This article discusses in great detail the definition
of glyph metrics, per se the TrueType specification, and the way they
are managed and used by the FreeType engine. This information is
crucial when it comes to rendering text strings, either in a
conventional (i.e. Roman) layout, or with vertical or right-to-left
ones. Some aspects like glyph rotation and transformation are
explained too.
Comments and corrections are highly welcome, and can be sent to the
FreeType developers list.
I. An overview of font files
In TrueType, a single font file is used to contain
information related to classification, modeling and rendering of text
using a given typeface. This data is located in various independent
`tables', which can be sorted in four simple classes, as described
below:
We call face data the amount of information related to a
given typeface, independently of any particular scaling,
transformation, and/or glyph index. This usually means some
typeface-global metrics and attributes, like family and styles,
PANOSE number, typographic ascenders and descenders, as well as
some very TrueType specific items like the font `programs' found
in the fpgm and prep tables, the gasp table,
character mappings, etc.
In FreeType, a face object is used to model a font file's
face data.
We call instance a given pointsize/transformation, at a
given device resolution (e.g. 8pt at 96x96dpi, or 12pt at
300x600dpi, etc). Some tables found in the font files are used to
produce instance-specific data, like the cvt table, or the
prep program. Though they are often part of the face data,
their processing results in information called instance
data.
In FreeType, it is modeled through an instance object,
which is always created from an existing face object.
We call glyph data the piece of information related to
specific glyphs. This includes the following things that are
described in more details in the next sections:
The FreeType engine doesn't map each glyph to a single structure,
as this would waste memory for no good reason. Rather, a glyph
object is a container, created from any active face,
which can be used to load and/or process any font glyph at any
instance (or even no instance at all). Of course, the glyph
properties (outline, metrics, bitmaps, etc.) can be extracted
independently from an object once it has been loaded or
processed.
Finally, there is a last class of data that doesn't really fit in
all others, and that can be called text data. It comprises
information related to the grouping of glyphs together to form
text. Simple examples are the kerning table, which
controls the spacing between adjacent glyphs, as well as some of
the extensions introduced in TrueType Open,
OpenType, and TrueType GX like glyph substitution
(ligatures, vertical representations), baseline management,
justification, etc.
This article focuses on the basic TrueType tables, and hence, will
only talk about kerning, as FreeType doesn't support OpenType nor
GX (yet). [Support for TrueType Open is already partially
available.]
II. Glyph Outlines
TrueType is a scalable font format; it is thus
possible to render glyphs at any scale, and under any affine
transform, from a single source representation. However, simply
scaling vectorial shapes exhibits at small sizes (where `small' refers
here to anything smaller than at least 150 pixels) a collection
of un-harmonious artifacts, like widths and/or heights
degradations.
Because of this, the format also provides a complete programming
language used to design small programs associated to each glyph. Its
role is to align the point positions on the pixel grid after the
scaling. This operation is hence called grid-fitting, or even
hinting.
The source format of outlines is a collection of closed paths
called contours. Each contour delimits an outer or inner
region of the glyph, and can be made of either line segments
and/or second-order beziers (also called conic beziers or
quadratics).
It is described internally as a series of successive points, with
each point having an associated flag indicating whether it is `on'
or `off' the curve. These rules are applied to decompose the
contour:
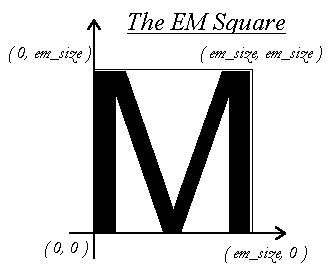
In creating the glyph outlines, a type designer uses an imaginary
square called the EM square. Typically, the EM square
encloses the capital letter `M' and most other letters of a
typical roman alphabet. The square's size, i.e., the number of
grid units on its sides, is very important for two reasons:
Note that glyphs can freely extend beyond the EM square if the
font designer wants this. The EM is used as a convenience, and is
a valuable convenience from traditional typography.
Under FreeType, scaled pixel positions are all expressed in the
26.6 fixed float format (made of a 26-bit integer mantissa, and a
6-bit fractional part). In other words, all coordinates are
multiplied by 64. The grid lines along the integer pixel
positions, are multiples of 64, like (0,0), (64,0), (0,64),
(128,128), etc., while the pixel centers lie at middle coordinates
(32 modulo 64) like (32,32), (96,32), etc.
As said before, simply scaling outlines to a specific instance
always creates undesirable artifacts, like stems of different
widths or heights in letters like `E' or `H'. Proper glyph
rendering needs that the scaled points are aligned along the pixel
grid (hence the name grid-fitting), and that important
widths and heights are respected throughout the whole font (for
example, it is very often desirable that the letters `I' and `T'
have their central vertical line of the same pixel width).
Type 1 PostScript font files include with each glyph a small
series of distances called hints, which are later used by
the type manager to try grid-fitting the outlines as cleverly as
possible. On one hand, it has the consequence that upgrading your
font engine can enhance the visual aspects of all fonts of your
system; on the other hand, the quality of even the best version of
Adobe's Type Manager isn't always very pleasing at small sizes
(notwithstanding font smoothing).
TrueType takes a radically different approach: Each glyph has an
associated `program', designed in a specific geometrical language,
which is used to align explicitly each outline point to the pixel
grid, preserving important distances and metrics. A stack-based
low-level bytecode is used to store it in the font file, and is
interpreted later when rendering the scaled glyphs.
This means that even very complex glyphs can be rendered perfectly
at very small sizes, as long as the corresponding glyph code is
designed correctly. Moreover, a glyph can loose some of its
details, like serifs, at small sizes to become more readable,
because the bytecode provides interesting features.
However, this also have the sad implication that an ill-designed
glyph code will always render junk, whatever the font engine's
version, and that it's very difficult to produce quality glyph
code. There are about 200 TrueType opcodes, and no known
`high-level language' for it. Most type artists aren't
programmers at all and the only tools able to produce quality code
from vectorial representation have been distributed to only a few
font foundries, while tools available to the public, e.g.
Fontographer, are usually expensive though generating average to
mediocre glyph code.
All this explains why an enormous number of broken or ugly `free'
fonts have appeared on the TrueType scene, and that this format is
now mistakenly thought as `crap' by many people. Funnily, these
are often the same who stare at the `beauty' of the classic `Times
New Roman' and `Arial/Helvetica' at 8 points.
Once a glyph's code has been executed, the scan-line converter
converts the fitted outline into a bitmap (or a pixmap with
font-smoothing).
III. Glyph metrics
The baseline is an imaginary line that is used to `guide' glyphs
when rendering text. It can be horizontal (e.g. Roman, Cyrillic,
Arabic, etc.) or vertical (e.g. Chinese, Japanese, etc).
Moreover, to render text, a virtual point, located on the
baseline, called the pen position, is used to locate
glyphs.
Each layout uses a different convention for glyph placement:
The pen position is always placed on the baseline in
TrueType, unlike the convention used by some graphics
systems, like Windows, to always put the pen above the line,
at the ascender's position.
A various number of face metrics are defined for all glyphs in
a given font. Three of them have a rather curious status in
the TrueType specification; they only apply to horizontal
layouts:
This is the distance from the baseline to the highest/upper
grid coordinate used to place an outline point. It is a
positive value, due to the grid's orientation with the
y axis upwards.
The distance from the baseline to the lowest grid coordinate
used to place an outline point. This is a negative value,
due to the grid's orientation.
The distance that must be placed between two lines of text.
The baseline-to-baseline distance should be computed as
if you use the typographic values.
The problem with these metrics is that they appear three times
in a single font file, each version having a slightly different
meaning:
All metrics are expressed in font units. If you want to use any
of the two first versions of these metrics, the TrueType
specification contains some considerations and computing tips
that might help you.
Other, simpler metrics are:
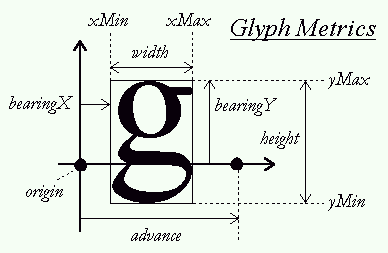
This is an imaginary box that encloses any glyph (usually as
tightly as possible). It is represented by four fields,
namely xMin, yMin, xMax, and
yMax, that can be computed for any outline. In
FreeType, their values can be in font units (if measured in
the original outline) or in 26.6 pixel units (if
measured on scaled outlines).
Note that if it wasn't for grid-fitting, you wouldn't need
to know a box's complete values, but only its dimensions to
know how big is a glyph outline/bitmapa. However, correct
rendering of hinted glyphs needs the preservation of
important grid alignment on each glyph translation/placement
on the baseline, which is why FreeType always returns the
complete glyph outline.
Note also that the font's header contains a global font
bounding box in font units which should enclose all glyphs
in a font. This can be used to pre-compute the maximum
dimensions of any glyph at a given instance.
This concept comes directly from the world of traditional
typography. It represents the amount of space within the
`leading' which is reserved for glyph features that lay
outside of the EM square (like accentuation). It usually
can be computed as
This is another name for the linegap.
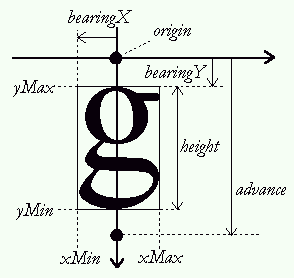
Each glyph has also distances called bearings and
advances. Their definition is constant, but their values
depend on the layout, as the same glyph can be used to render
text either horizontally or vertically.
This is the horizontal distance from the current pen
position to the glyph's left bounding box edge. It is
positive for horizontal layouts, and most generally negative
for vertical one.
This is the vertical distance from the baseline to the top
of the glyph's bounding box. It is usually positive for
horizontal layouts, and negative for vertical ones
This is the horizontal distance the pen position must be
incremented (for left-to-right writing) or decremented (for
right-to-left writing) by after each glyph is rendered when
processing text. It is always positive for horizontal
layouts, and null for vertical ones.
This is the vertical distance the pen position must be
decremented by after each glyph is rendered. It is always
null for horizontal layouts, and positive for vertical
layouts.
The glyph's horizontal extent. More simply, it is
(bbox.xMax - bbox.xMin) for unscaled font coordinates.
For scaled glyphs, its computation requests specific care,
described in the grid-fitting chapter below.
The glyph's vertical extent. More simply, it is
(bbox.yMax - bbox.yMin) for unscaled font coordinates.
For scaled glyphs, its computation requests specific care,
described in the grid-fitting chapter below.
Only used for horizontal layouts to describe the distance
from the bbox's right edge to the advance width. It is in
most cases a non-negative number. The FreeType library
doesn't provide this metric directly, as it isn't really
part of the TrueType specification. It can be computed
simply as
Finally, if you use `ABC widths' under Windows and OS/2, the
following relations apply:
All these metrics are stored in font units in the font file.
They must be scaled and grid-fitted properly to be used at a
specific instance. This implies several things:
If you don't need the exact fitted value, it's much faster
to query the metrics in font units, then scale them to the
instance's dimensions.
Another very important consequence of grid-fitting is the fact
that moving a fitted outline by a non-integer pixel distance
will simply ruin the hinter's work, as alignments won't be
preserved. The translated glyph will then look `ugly' when
converted to a bitmap!
In other words, each time you want to translate a fitted glyph
outline, you must take care of only using integer pixel
distances (the x and y offsets must be multiples
of 64, which equals to 1.0 in the 26.6 fixed float
format).
If you don't care about grid-fitting (typically when rendering
rotated text), you can use any offset you want and use sub-pixel
glyph placement.
IV. Text processing
This section demonstrates how to use the concepts previously defined
to render text, whatever the layout you use.
We will start by generating a simple string with a Roman alphabet.
The layout is thus horizontal, left to right.
For now, we will assume all glyphs are rendered in a single target
bitmap. The case of generating individual glyph bitmaps, then
placing them on demand on a device is presented in a later chapter
of this section.
Rendering the string needs to place each glyph on the baseline;
this process looks like the following:
If you don't want to access the outline in your code, you can
also use the API function TT_Get_Glyph_Bitmap() which does the
same as the previous lines:
Generating strings for different layouts is very similar. Here
are the most important differences.
The main difference here is that, as the advance width and
left side bearings are oriented against the flow of text, the
pen position must be decremented by the advance width,
before placing and rendering the glyph. Other than
that, the rest is strictly similar.
In this case, the baseline is vertical, which means that the
pen position must be shifted in the vertical direction. You
need the vertical glyph metrics to do that (using the
TT_Get_Big_Glyph_Metrics() function).
Once you get these, the rest of the process is very similar.
The glyph outline is placed relative to an imaginary origin of
(0,0), and you should translate it to the pen position before
rendering it.
The big difference is that you must decrement pen_y, rather
than increment pen_x (this is for the TrueType convention of y
oriented upwards).
Loading each glyph when rendering text is slow, and it's much
more efficient to render each one in a standalone bitmap to place
it in a cache. Text can then be rendered fast by applying simple
blit operations on the target device.
To be able to render text correctly with the bitmaps, you must
record and associate with them its fitted bearings and advances.
Hence the following process:
NOTE 2:
Don't forget to shift it by (-xMin, -yMin) to fit it in
the bitmap:
The previously described rendering processes all align glyphs on
the baseline according to metrics fitted for the display's
distance. In some cases, the display isn't the final output, and
placing the glyphs in a device-independent way is more important
than anything.
A typical case is a word processor which displays text as it
should appear on paper when printed. As you've probably noticed,
the glyphs aren't always spaced uniformly on the screen as you
type them, sometimes the space between an `m' and a `t' is too
small, some other it is too large, etc.
These differences are simply due to the fact that the word
processor aligns glyphs in an device-independent way, using
original metrics in font units to do it, then scale them as it
can to display text on screen, usually at a very smaller
resolution than your printer's one.
Device-independence is a crucial part of document portability,
and it is very saddening to see that most professional word
processors don't do it correctly. For example, MS Word uses
the fitted metrics of the printer's resolution, rather than the
originals in font units.
This is great to get sure that your text prints very well on your
printer, but it also implies that someone printing the exact same
document on a device with different output resolutions (e.g.
bubble-jet vs. laser printers) may encounter trouble.
As the differences in advances accumulate on one line, they can
sum to the width of one or more glyphs in extreme cases, which is
enough to `overflow' the automatic justification algorithm. This
may add additional lines of printed text, or even remove some.
Moreover, supplemental lines can produce unexpected page breaks
and `blank' pages. This can be extremely painful when working
with large documents, as this `feature' may require you to
redesign completely your formatting to re-print it.
In conclusion, if you want portable document rendering, never
hesitate to use and apply device-independent terms! For example,
a simple way to produce text would be:
An interesting effect that most people appreciate is
kerning. It consists of modifying the spacing between two
successive glyphs according to their outlines. For example, the
letters `T' and a `y' can be easily moved closer, as the top of
the `y' fits nicely under the `T's upper right bar.
To perform kerning, the TrueType specification provides a
specific table (its tag being `kern'), with several storage
formats. This section doesn't explain how to access this
information; however, you can have a look at the standard
extension called `ttkern.h' which comes with FreeType.
The kerning distance between two glyphs is a value
expressed in font units which indicates whether their outline can
be moved together or apart when one follows the other. The
distance isn't reflexive, which means that the kerning for the
glyph pair (`T',`y') isn't the same as the one for (`y',`T').
The value is positive when the glyphs must be moved apart, and
negative when they must be moved closer. You can implement
kerning simply by adding its scaled and rounded value to the
advance width when moving the pen position. Here an example for
horizontal kerning:
In order to produce rotated glyphs with FreeType, one must
understand a few things:
These flags can be interpreted by the glyph code to toggle certain
processings which vary from one font to the other. However, most
of the TrueType fonts that were tested with FreeType, if not all
of them, simply change the dropout-mode when any of these flags is
set, and/or disable hinting when rotation is detected. We advise
you to never set these flags, even when rotating text. For what
it's worth, hinted rotated text is no uglier than un-hinted
one.
You can use the function TT_Set_Instance_Transform_Flags() to set
them. Then, rendering can be done with the following calls:
Do not grid-fit the pen position before rendering your glyph when
rendering rotated text. If you do, your transformed baseline
won't be preserved on each glyph, and the text will look like it's
`hopping' randomly. This is particularly visible at small
sizes.
Sub-pixel precision placement is very important for clean
rotated text.
The FreeType engine's scan-line converter (the component also
called the rasterizer) is able to convert a vectorial glyph
outline into either a normal bitmap, or an 8-bit pixmap (a.k.a.
colored bitmaps on some systems). This last feature is
called gray-level rendering or font-smoothing,
because it uses a user-supplied palette to produce anti-aliased
versions of the glyphs.
Its principle is to render a bitmap which is twice as large than
the target pixmap, then simply filtering it using a 2x2
summation.
FreeType's scan-line converter doesn't use or need an intermediate
second bitmap. Rather, filtering is performed in a single pass
during the sweep (see the file `raster.txt' for more information
about it).
You'll notice that, as with Windows 95, FreeType's rasterizer
only grays those parts of the glyph which need it, i.e., diagonals
and curves, while keeping horizontal and vertical stems straight
`black'. This greatly improves the legibility of text, while
avoiding the `blurry' look anti-aliased fonts typically found with
Adobe's Type Manager or Acrobat.
There are thus five available gray-levels, ranging from 0
to 4, where level 0 and level 4 are the background
and foreground colors, respectively, and where levels 1,
2, 3 are intermediate. For example, to render black text on
a white background, one can use a palette like:
To set the engine's gray-level palette, simply use the API
function TT_Set_Raster_Palette() after initialization. It expects
an array of 5 chars which will be used to render the
pixmaps.
Note that the rasterizer doesn't create bitmaps or pixmaps.
Rather, it simply renders glyphs in the arrays you pass to it.
The generated glyph bitmaps are simply `or'-ed to the target (with
0 being the background as a convention); in the case of pixmaps,
pixels are simply written to the buffer, in spans of four aligned
bytes.
The raster isn't able to superpose `transparent' glyphs on the
target pixmap. This means that you should always call the API
functions TT_Get_Glyph_Pixmap() and TT_Get_Outline_Pixmap() with
an empty map, and perform the superposition yourself.
This can be more or less tricky, depending on the palette you are
using and your target graphics resolution. One of the components
found in the test directory, called `display.c', has large
comments on the way it implements it for the test programs. You
are encouraged to read the test program sources to understand how
one can take advantage of font smoothing.
Pixmap surimposition is too system-specific a feature to be part
of the FreeType engine. Moreover, not everybody needs it!
Finally, the question of sur-imposing anti-aliased colored text on
any texture, since being even more tricky, is left as an exercise
to the reader ;-) If this topic really interests you, the
FreeType mailing list may host some helpful enthusiasts ready to
answer your questions. Who knows :-)
Substitution is used to replace one glyph by another when some
specific condition is met in the text string. Its most common
examples are ligatures (like replacing the `f' followed by `i'
by the single glyph `fi' if available in the font), as well as
positional selection as performed in the Arabic script (for
those not aware of this, each letter of the Arabic alphabet
can be written differently according to its position on words:
starting, ending, intermediate, or isolated).
The base TrueType format doesn't define any table for glyph
substitution. However, GX, TrueType Open, and OpenType
provide (incompatible) extensions to perform it. Of course,
it isn't supported by the engine, but an extension could be
easily written to access the required tables.
[Support for TrueType Open is already partially available.]
...
* # on
* off
__---__
#-__ _-- -_
--__ _- -
--__ # \
--__ #
-#
Two `on' points
Two `on' points and one `off' point
between them
*
# __ Two `on' points with two `off'
\ - - points between them. The point
\ / \ marked `0' is the middle of the
- 0 \ `off' points, and is a `virtual
-_ _- # on' point where the curve passes.
-- It does not appear in the point
list.
*
 Each glyph's original outline points are located on a grid of
indivisible units. The points are stored in the font file as
16-bit integer grid coordinates, with the grid origin's being at
(0,0); they thus range from -16384 to 16383.
Each glyph's original outline points are located on a grid of
indivisible units. The points are stored in the font file as
16-bit integer grid coordinates, with the grid origin's being at
(0,0); they thus range from -16384 to 16383.
IMPORTANT NOTE:

IMPORTANT NOTE: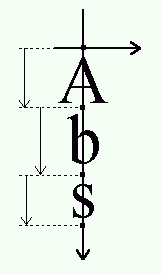
A = left side bearing
B = width
C = right side bearing
A+B+C = advance width
IMPORTANT NOTE:
To be continued...
pen_x = cursor_x;
pen_y = cursor_y;
TT_Load_Glyph( instance,
glyph,
glyph_index,
TTLOAD_DEFAULT );
TT_Get_Glyph_Metrics( glyph, &metrics );
TT_Get_Glyph_Outline( glyph, &outline );
( pen_x, pen_y )
To place it on its correct position, you can use the call
TT_Translate_Outline( outline, pen_x, pen_y );
TT_Get_Outline_Bitmap( outline, &target_bitmap );
IMPORTANT NOTE:
TT_Get_Glyph_Outline( glyph, &outline );
TT_Translate_Outline( outline, x_offset, y_offset );
TT_Get_Outline_Bitmap( outline, &target_bitmap );
TT_Translate_Outline( outline, -x_offset, -y_offset );
is equivalent to:
TT_Get_Glyph_Bitmap( glyph,
x_offset,
y_offset,
&target_bitmap );
pen_x += metrics.advance;
The advance being grid-fitted, the pen position remains
aligned on the grid.
pen_y -= metrics.advance;
TT_Load_Glyph( instance,
glyph,
glyph_index,
TTLOAD_DEFAULT );
TT_Get_Glyph_Metrics( glyph, &metrics );
The bbox is always fitted when calling
TT_Get_Glyph_Metrics() on a hinted glyph. You can then
easily compute the glyph's dimension in pixels as:
width = (bbox.xMax - bbox.xMin) / 64;
height = (bbox.yMax - bbox.yMin) / 64;
NOTE 1:
The fitted bounding box always contains all the dropouts
that may be produced by the scan-line converter. This
width and height are thus valid for all kinds of
glyphs).
If you want to compute the dimensions of a rotated
outline's bitmap, compute its bounding box with
TT_Get_Outline_BBox(), then grid-fit the bbox manually:
#define FLOOR(x) ((x) & -64)
#define CEILING(x) (((x)+63) & -64)
xMin = FLOOR(xMin);
yMin = FLOOR(yMin);
yMin = CEILING(xMax);
yMax = CEILING(yMax);
then compute width and height as above.
bitmap.width = width;
bitmap.cols = (width+7) & -8;
bitmap.rows = height;
bitmap.flow = TT_Flow_Up;
bitmap.size = bitmap.cols * bitmap.rows;
bitmap.buffer = malloc( bitmap.size );
/* Note that the offsets must be grid-fitted to */
/* preserve hinting! */
TT_Get_Glyph_Bitmap( glyph,
&bitmap,
-bbox.xMin,
-bbox.yMin );
bearingX / 64 = left side bearing in pixels
advance / 64 = advance width/height in pixels
When your cache is set up, you can then render text using a
scheme similar to the ones describe in 1. and 2.,
with the exception that now pen positions and metrics are
expressed in pixel values. We are done!
pen_x = cursor_x;
pen_y = cursor_y;
while ( glyph_to_render )
{
access_cache( glyph_index, metrics, bitmap );
blit_bitmap_to_position
( pen_x + bearingX,
pen_y (+ bearingY depending on orientation ) );
pen_x += advance;
}
#define ROUND( x ) ( (x + 32) & -64 )
scaled_kerning = kerning * imetrics.x_scale / 0x10000;
pen_x += metrics.advance + ROUND( scaled_kerning );
/* set the flags */
TT_Set_Instance_Transforms( instance,
rotated,
stretched );
/* load a given glyph */
TT_Get_Glyph_Outline( instance,
glyph,
index,
TTLOAD_DEFAULT );
/* access its outline */
TT_Get_Glyph_Outline( instance, &outline );
/* in order to transform it */
TT_Transform_Outline( outline, &matrix );
/* and/or */
TT_Translate_Outline( outline,
x_offset, y_offset );
/* to render it */
TT_Get_Outline_Bitmap( outline, &bitmap );
Here is an example, assuming that the following variables
TT_Matrix matrix; /* 2x2 matrix */
TT_Pos x_off, y_off; /* corrective offsets */
define a transformation that can be correctly applied to a glyph
outline which have been previously placed relative to the
imaginary point position (0,0) with bearings preserved. Rendering
text can now be done as follows:
pen_x = cursor_x;
pen_y = cursor_y;
TT_Transform_Outline( outline, &matrix );
TT_Translate_Outline( outline,
pen_x + x_off,
pen_y + y_off );
(Note that the transformation offsets have been included in
the translation.)
vec_x = metrics.advance;
vec_y = 0;
TT_Transform_Vector( &vec_x, &vec_y, &matrix );
pen_x += vec_x;
pen_y += vec_y;
IMPORTANT NOTE:
NOTE:
palette[0] = white (background)
palette[1] = light gray
palette[2] = medium gray
palette[3] = dark gray
palette[4] = black (foreground)
NOTE: